Adaboost 中文名叫自适应提升算法,是一种boosting算法。
boosting算法的基本思想
对于一个复杂任务来说,单个专家的决策过于片面,需要集合多个专家的决策得到最终的决策,通俗讲就是三个臭皮匠顶个诸葛亮。
对于给定的数据集,学习到一个较弱的分类器比学习到一个强分类器容易的多,boosting就是从弱学习器出发,反复学习,得到多个弱分类器,最后将这些弱分类器组合成强分类器。
boosting算法需要解决两个问题
每一轮如何改变训练样本的权重
如何将弱分类器组合成强分类器
adaboost是这样做的
1. 提高那些被前一轮弱分类器错误分类的样本的权值,而降低那些被正确分类样本的权值.,这样下个分类器就能专注于那些不好识别的样本,针对性的建立分类器。
2. 对于若分类器的组合,adaboost采取加权多数表决的方式,即加大分类错误率较小的弱分类器的权值,使其在表决中起较大作用,减小分类错误率较高的弱分类器的权值,使其在表决中起较小作用,
这可以理解为有些专家比较权威,他的意见要多采纳,有些只是不知名的专家,可以少采纳。
adaboost其实是一个加法模型,损失函数是指数损失函数,学习算法为前向分步算法的二分类学习方法。(其他学习算法如梯度下降)
加法模型
xgboost中其实也是加法模型,应该说boosting算法都是加法模型,而且还有很多算法也是加法模型,那什么是加法模型?
顾名思义,一个模型是由多个模型相加而得

那最终问题转化为基于加法模型的损失最小化,即

通常这是一个十分复杂的优化问题,想要一步到位非常困难,如用梯度下降,所以就有了前向分步算法。
前向分步算法
前向分步算法是一种优化算法,可以解决上面加法模型的问题。
大致思路是,从前向后,每一步学习一个基分类器,使得整体损失函数更小一点,从而逐步逼近全局最小值。
算法流程

解释一点: 新的学习器fm是在上个学习器fm-1的基础上学习的,也就是说在学习fm时fm-1已经确定,所以求L(y, fm)的极小值就是求b(x;r)的极小值,即单个学习器的最小值。
实际上这和梯度下降的思路十分相似,每次减小一点,逼近一点,而且形式也一样 fm=fm-1+βb
adaboost算法流程


误差解释
1. 误差计算时除以了Σw,因为每轮迭代时,Σw是一个固定值,而且后面会说明其实它等于1,所以不用除这个。
2. 误差计算时,分类正确为0,其权重被忽略,分类错误为1,其权重累加,所以是I(G!=y)
分类器权重解释

权重更新解释

组合分类器解释
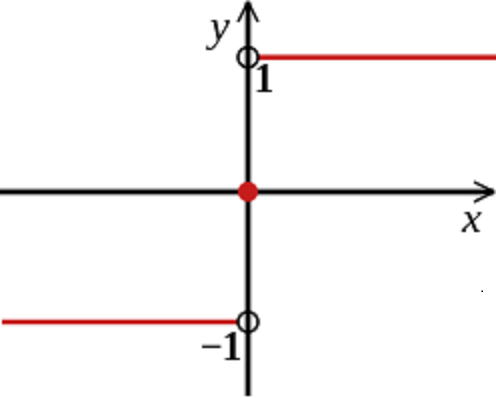
sign函数只能取1和-1,故adaboost为二分类。
当然可以通过修改实现多分类。
adaboost有很多种算法,但都大同小异,而且adaboost可以做回归,思路也是大同小异,具体请百度
adaboost进阶
正则化
adaboost每个学习器都是弱学习器,为什么还要正则化?其实不是正则化基学习器
fm=fm-1+αb(x,r),这是加法模型,α为基学习器的系数,可以理解为权重,
正则化是对加法模型增加一个学习率v,即fm=fm-1+vαb(x,r),这种方法适合于很多集成学习。
基分类器随机化
像随机森林一样,随机选特征,随机选样本
总结
理论上来讲,adaboost的弱学习器可以是任何模型,但用的最多的是决策树和神经网络,决策树是cart树
优点:精度高,不容易过拟合
缺点:对异常值敏感,因为异常值可能获得较大权重,最终影响整个模型
参考资料:
https://www.cnblogs.com/liuwu265/p/4693113.html?ptvd
https://zhuanlan.zhihu.com/p/59751960
https://zhuanlan.zhihu.com/p/42915999
https://blog.csdn.net/hahaha_2017/article/details/79852363
https://blog.csdn.net/guyuealian/article/details/70995333 原理-实例-代码(简明易懂)